Число́ — це абстрактна сутність, що використовується для опису кількості.

 

Типи чисел

Існують різні типи (множини) чисел.
Послідовність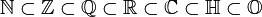

Натуральні числа

Натуральні числа 1,2,... використовуються при лічбі об'єктів. Множина натуральних чисел позначається .

Цілі числа

Якщо до натуральних чисел додати ще від'ємні числа та нуль, то ми отримаємо цілі числа . Цілі числа в математиці вивчають в рамках теорії чисел.

 Раціональні числа

Відношення між цілими і натуральними числами називається раціональними числами, або звичайними дробами. Множина всіх раціональних чисел позначається .

 Дійсні числа

Якщо до раціональних чисел додати всі нескінченні і неперіодичні десяткові дроби, так звані ірраціональні числа, то ми отримаємо дійсні числа .

 Комплексні числа

Дійсні числа, в свою чергу, можуть бути розширені до комплексних чисел .

 Інші типи чисел

Комплексні числа можуть бути розширені до кватерніонів . Необхідно відмітити, що для кватерніонів втрачається комутативність при множенні.

В свою чергу октоніни 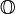є розширенням кватерніонів, і втрачають властивість асоціативності.

В математиці для множин існує величина - потужність множини, аналогічна кількості елементів в множині для скінченних множин. Розширення потужності на нескінченні множини призвело до подальшого узагальнення поняття числа. Зараз говорять про кардинали або, що те саме, кардинальні числа, котрі описують множини із будь-якої кількості елементів - скінченного чи нескінченного.